この記事は TeX & LaTeX Advent Calendar 2024 の3日目の記事です。2日目は津茶利休さんでした。 4日目はutさんです。

【目次】

大学入学共通テスト（旧センター試験）で「情報Ⅰ」が必須に！

基数変換計算練習帳を作る

生成物のサンプル

実装の話

補数計算練習帳を作る

生成物のサンプル

実装の話

ソースコード

基数変換計算練習帳

補数計算練習帳

大学入学共通テスト（旧センター試験）で「情報Ⅰ」が必須に！

今年度の受験生が2025年1月に受験する大学入学共通テスト（旧センター試験）から，情報Ⅰが全国の国公立大学で受験必須となりました。これまでも高校に「情報」という科目はありましたが，家庭科や美術などと同様の，「受験では使わない科目」扱いでした。それが，これからは，文系・理系を問わず，国公立大学を受験する全受験生が共通テストで必修となったわけで，新学習指導要領（新課程）における最も影響が大きな変化と言えるでしょう。

よく，「ITパスポートや基本情報技術者試験と比べてどちらが難しいですか？」と聞かれることがありますが，主に社会人を対象とするそれらの試験とは範囲が少し異なるので，一概に比較することは困難です。それらの試験でよく出てくる，次のような“業務っぽい”トピックは，高校生向けの科目である「情報Ⅰ」には含まれません。

損益計算書
労働者派遣法
ISMS内部監査
SWOT分析
単体テストと結合テスト

一方，もっと“情報科学っぽい”分野や仮説検定などの“統計っぽい”分野は，それらのIPA試験と比べると少し詳しめかもしれません。トピックの選別は教科書会社によって違いますが，次のような話題が扱われることもあります。

補数計算
半加算器と全加算器
CPUレジスタ
Shift-JIS / EUC-JP / ISO-2022-JP
パリティビット
モンテカルロ法や二分探索法のコード
ランレングス符号化・ハフマン符号化
ルーティングテーブル
VLAN
PKI（公開鍵基盤）
SQL
尺度水準
回帰分析
仮説検定

さて，多くの受験生にとってネックになりがちなのは，計算が絡んでくる，2進法/16進法や，補数計算の部分です。ここについては，単語暗記だけで済ませることはできず，手を動かして計算に慣れなければなりません。手を動かせば動かすほど体で覚えてくるものですから，嫌というほど計算練習ができるよう，LaTeXを使ってそれらの計算練習帳をランダム生成してみましょう。

基数変換計算練習帳を作る

まずは2進・10進・16進の基数変換全パターンに習熟しましょう。

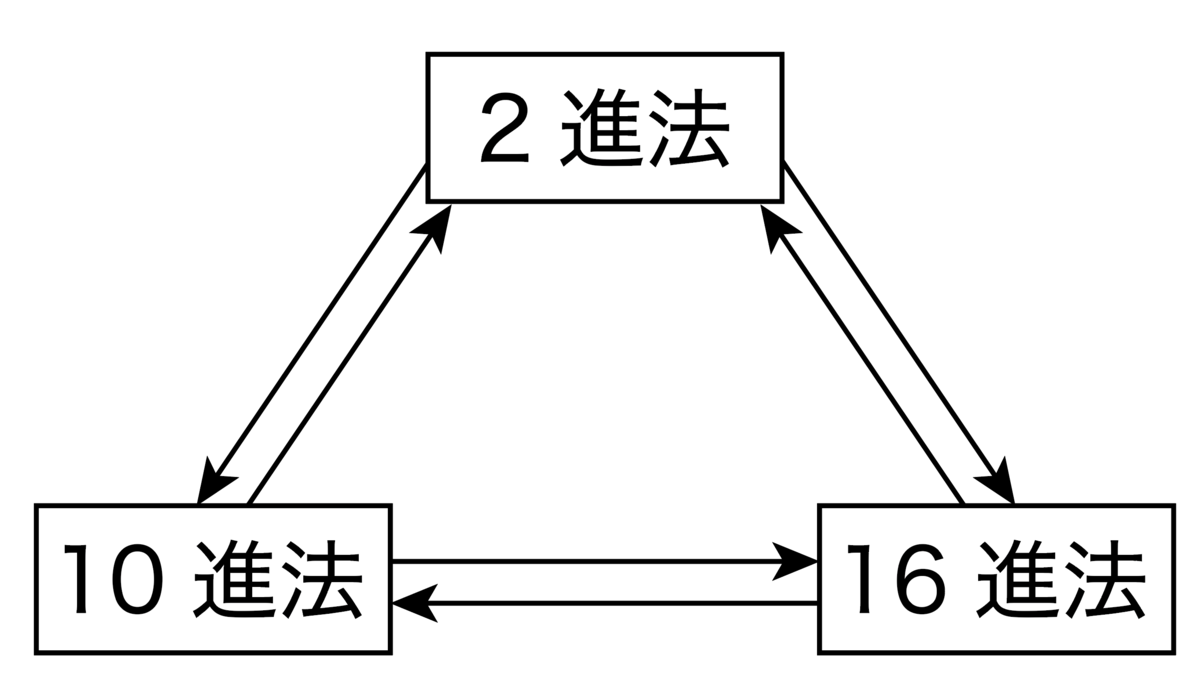
ここでは，expl3 on LaTeX を使ってこれらの基数変換問題のランダム生成，およびその解答の自動生成を行います。また，2進法や16進法の筆算による加法・減法，また bitwise-AND/OR/XOR演算にも慣れておくため，それらの問題もランダム生成しましょう。桁数が少ないEASY版と，桁数が多く計算が大変なHARD版の2種類を用意します。

生成物のサンプル

実装の話

expl3 には，\int_to_bin:n や \int_to_Hex:n という基数変換のための関数が用意されているので，基数変換自体の実装は簡単です。表示のための 0-padding や，bitwise演算の実装の方が少し手間がかかります。bitwise演算については，\int_mod:nn によって2で割った余りを求めることで最下位ビットを取り出し，\int_div_truncate:nn で2で割ることでビットシフトするというのを繰り返し，1桁ずつ愚直にビット演算していきます。